To get the count of a specific keyword or a term from the contents of a file, we can use the cat command followed by the path to the file, then the | operator (aka pipe operator), then the grep command, then the keyword you want to search for and finally the -c flag (count flag) in the Linux terminal.
TL;DR
# Get the count of a specific
# word from the contents of a file
cat <PATH_TO_FILE> | grep <YOUR_SEARCH_TERM> -c
For example, let's say we have a file called myFile.txt which has some content like below,
Example Content
Wikipedia is a free content, multilingual online encyclopedia
written and maintained by a community of volunteer contributors
through a model of open collaboration, using a wiki-based editing system.
Wikipedia was launched on January 15, 2001, by Jimmy Wales
and Larry Sanger; Sanger coined its name as a blending of "wiki" and "encyclopedia".
Initially available only in English, versions in other languages were quickly developed.
Its combined editions comprise more than 57 million articles,
attracting around 2 billion unique device visits per month,
and more than 17 million edits per month (1.9 edits per second).
Now, we want to find the number of times a specific word occurred or count of the word Wikipedia from the contents of the myFile.txt file. We can do that using the cat and grep commands like this,
# Get the count of a specific
# word from the contents of a file
cat myFile.txt | grep Wikipedia -c
The output of running the above command may look like this,
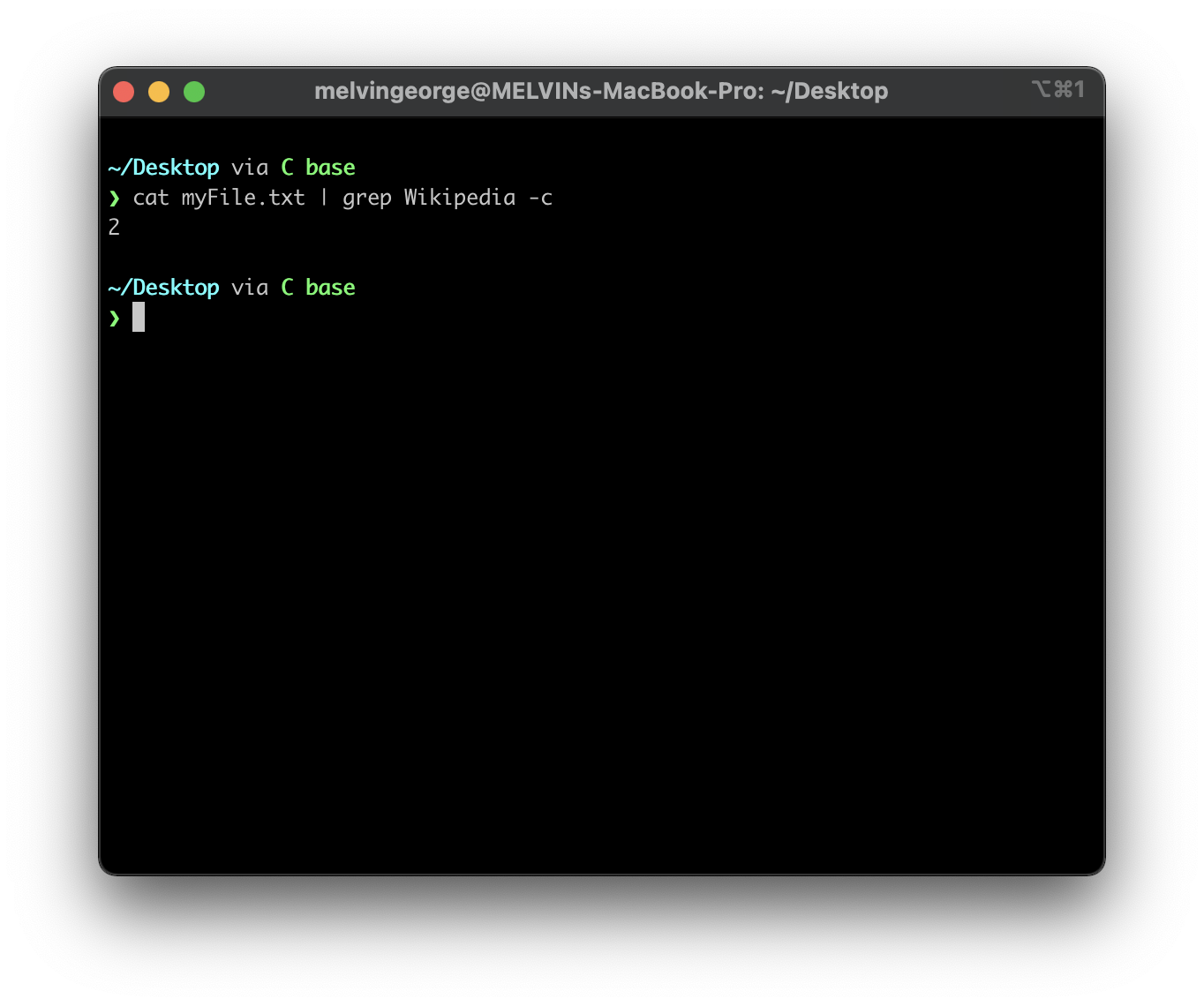
As you can see that the word Wikipedia has a count of 2 in the above output.
See the execution of the above command live in repl.it.
That's all 😃!